Is the future of Neural Networks Sparse? An Introduction (1/N)
From principles to real-world library support.

Hi, I am François Lagunas.
I am doing Machine Learning research, and I have been working for the last months on using sparse matrices, especially in Transformers. The recent announcement that OpenAI is porting its block sparse toolbox in PyTorch is really big news:
“We are in the process of writing PyTorch bindings for our highly-optimized blocksparse kernels, and will open-source those bindings in upcoming months.”
I was talking about it with the outstanding Hugging Face team, (I am one of their early investors), and I wanted to share with you my excitement!
What is a Sparse Matrix?
A sparse matrix is just a matrix with some zeros. Usually, a lot of them. So every place you are using a dense matrix, in a linear layer, for example, you could be using a sparse one.
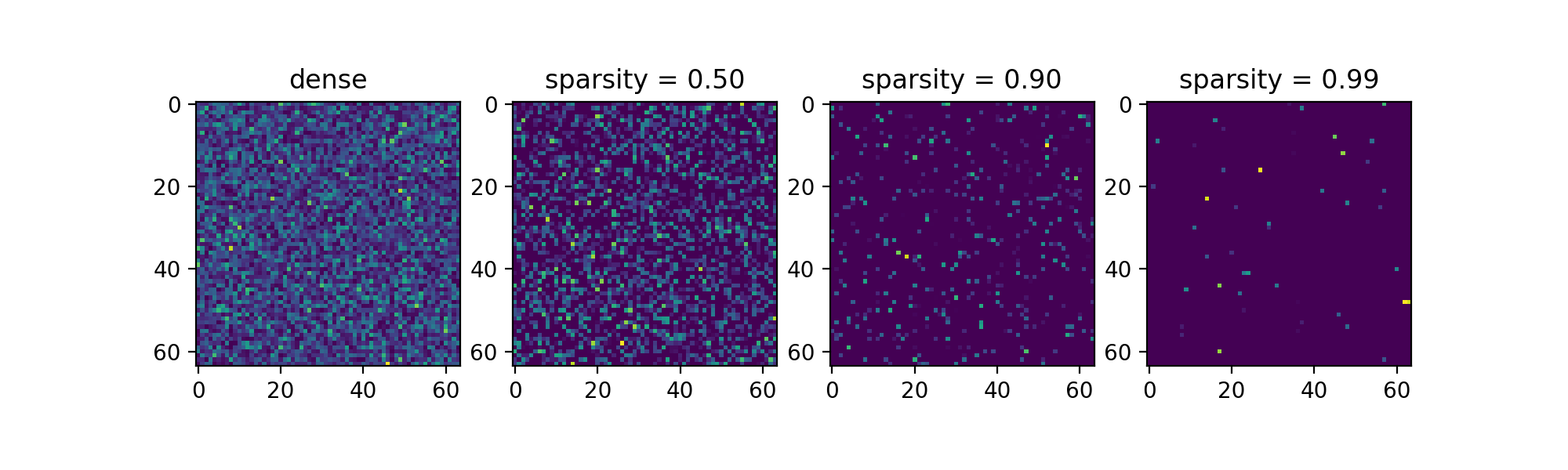
The sparsity of the matrix is the fraction of zeros against the size of the matrix
The pros? If you have a lot of zeros, you don’t have to compute some multiplications, and you don’t have to store them. So you may gain on size and speed, for training and inference (more on this today).
The cons? Of course, having all these zeros will probably have an impact on network accuracy/performance. But to what extent? You may be surprised.
Where are they from?
The first researchers/engineers to use sparse matrices were Finite Elements users.
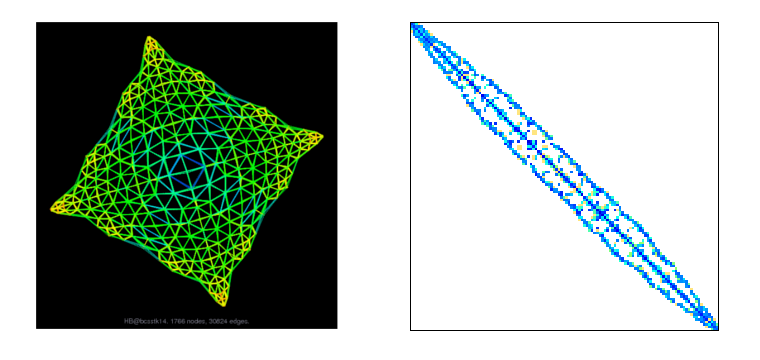
When you have to deal with large physical simulations, you get a large graph of interconnected vertices.
Each vertex is a point of your system, and each edge connects two vertices. That means that these two points will have some influence on each other in the model. And so there is a non-zero value in the matrix that describes the graph.
This last sentence sums it up: you need non-zero values in the matrix when two dimensions are interacting in some way.
**Now getting back to ML, you should ask yourself the same question: are all the dimensions of my input vector interacting with all the others? **Usually not. So going sparse maybe useful.
We have actually a very good, and famous, example of a successful trip to sparse-land: convolutional layers.

Convolutional layers are a smart and efficient way to implement a sparse transformation on an input tensor.
When processing images, it comes down to two things:
Sparsity: the transformation is local → each output pixel should depend on a few neighboring input pixels.
Invariance: the transformation does not depend on the position in the image
Then you just add the constraint that the transformation is linear: if you were to represent this transformation, you would get a HUGE matrix with only a few non-zeros. But of course, the right way to do this is to do a multiplication of the input tensor with a small set of small matrices (each square in the image before).
The importance of convolutions in today’s ML success is obvious. But you can see that finding a clever way to make things sparse sounds like a good recipe to save time and space.
Where are they useful?
Convolutions are already an efficient form of sparsity, so you could try to make them even more sparse, but some other networks contain much larger matrices that may benefit from sparsity: Transformers.
And those are getting bigger and bigger. We have greatly exceeded the 1 billion parameters in 2019, and it’s not stopping here. The cost to train and to use those networks is getting unpractical, so every method to reduce their size will be welcome.
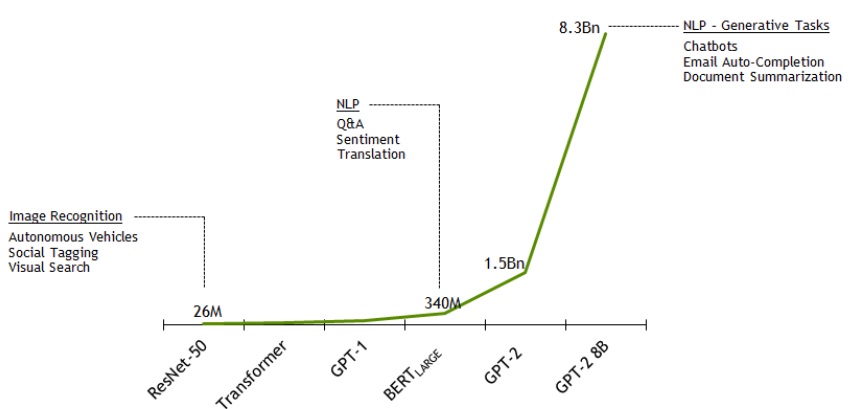
Why the OpenAI announcement is so important?
So, if everything is fine in sparse-land, we should all be trying sparse matrices, shouldn’t we?
Yes. But there is this stupid thing called implementation. It’s easy to see the theoretical improvements we could get with sparse compute. But the support in libraries is quite … sparse.
PyTorch developers, for example, have done a significant effort to support sparse compute. But there is still a big gap in performance between dense and sparse matrices operations, which defeats the whole purpose of using them. Even memory usage is quite large: sparsity has to be more than 80% to save some room on sparse matrices (more on that in my next post). Even basic serialization was broken before version 1.4. The reason is that the underlying libraries (for example cuSPARSE) are not doing a great job because the problem is ill-suited to the way GPU works.
So the OpenAI announcement on their block sparse tools is very good news for those who want to use sparse ops without sacrificing training speed (and it looks like some people have been waiting for some time now). And we are not talking about a few percents.
“Our kernels typically performed one or two orders of magnitude faster in terms of GFLOPS.”
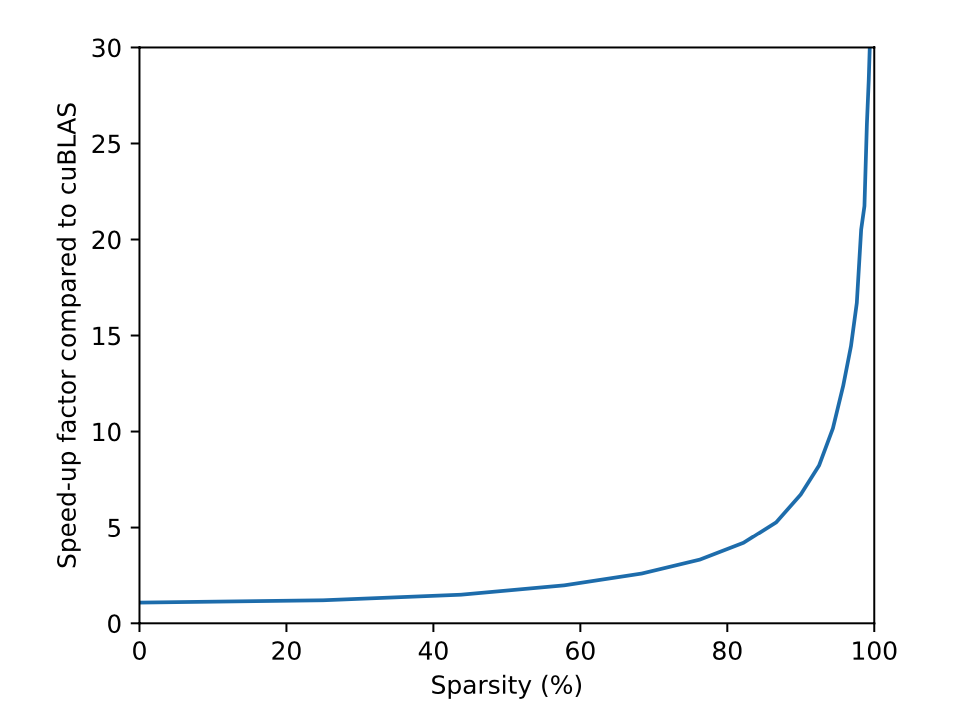
The worst thing is that the paper concludes that cuBLAS is faster that cuSPARSE even with very sparse matrices. How sad.
The magic keyword here is “block”. It’s hard to implement general sparse matrice computations on GPUs in an efficient way. But it gets much easier if you add a “reasonable” constraint on the form of the matrices: their non-zeros should be grouped in small fixed-size blocks, and that makes GPU processing much easier to parallelize efficiently. Typically 8x8, 16x16 or 32x32 blocks, 16x16 already giving a very good performance, with 32x32 giving a slightly better one.
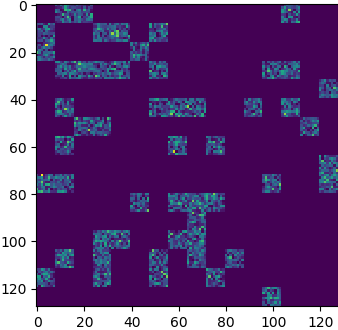
Of course, the “block” constraint may be crippling some sparsification algorithms, or at least it would require some changes to take it into account.
But at least we can play with large high sparsity matrices, and the block constraint may not be a big issue: if you think about it, it means that there is some locality in the dimensions, and that sounds a quite reasonable constraint. That’s the same reason band matrices have been useful in the past (finite difference, finite elements), and it was a much stronger constraint.
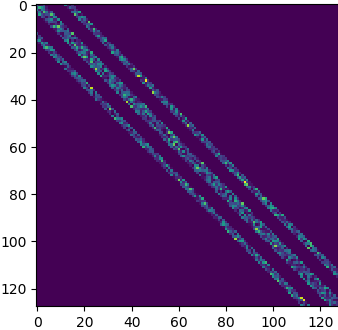
Conclusion
I hope I have convinced you that 2020 will be the sparse network year (it already has two zeros, that’s a sign).
Next time for those who are curious about what happens when they are using some CUDA based PyTorch code, we’ll dig a bit deeper in GPU internals, (and we will understand why block sparse code is outrunning sparse code by a large margin).
This article series will continue on the different techniques that have been proposed to make sparse networks, and what are the potential long term benefits.
More reading
First, here is a study of PyTorch sparse performance.
If you want to have a very detailed review of different complementary approaches to network size reduction, and not just about sparse ones, you should definitely read this article.
And if you want to create illustrations like the header of this blog post, you will find the code I used on my github.
